ул.Симферопольская
дом 5, офис 9
![]() Корзина
Корзина
Корзина пуста
1. Линейные электрические цепи постоянного тока. 1, 2 законы Кирхгофа. Уравнение кирхгофа для цепи постоянного тока
Основные законы цепей постоянного тока
Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.
Закон Ома для участка цепи
Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома
Рис.1 или UR = RI.
В этом случае UR = RI – называют напряжением
или падением напряжения на резисторе R, а – током в резисторе R.
При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:
.
В этом случае закон Ома для участка цепи запишется в виде:
I = Uq.
Закон Ома для всей цепи
Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис.1), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:
.
Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.
Первый закон Кирхгофа
В любом узле электрической цепи алгебраическая сумма токов равна нулю
,
где m – число ветвей подключенных к узлу.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1) I - I1 - I2 = 0.
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках
,
где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rк в контуре; Uк = RкIк – напряжение или падение напряжения на к-м элементе контура.
Для схемы (рис. 1) запишем уравнение по второму закону Кирхгофа:
E = UR + U1.
Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю
.
При записи уравнений по второму закону Кирхгофа необходимо:
1) задать условные положительные направления ЭДС, токов и напряжений;
2) выбрать направление обхода контура, для которого записывается уравнение;
3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.
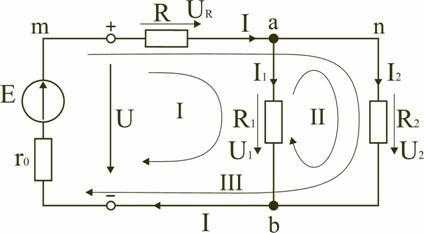 Рис.2
Рис.2
Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2):
контур I: E = RI + R1I1 + r0I,
контур II: R1I1 + R2I2 = 0,
контур III: E = RI + R2I2 + r0I.
В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
W = I2Rt.
Скорость преобразования электрической энергии в другие виды представляет электрическую мощность
.
Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.
.
Это соотношение (1.8) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в (1.8) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в (1.8) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:
EI = I2(r0 + R) + I12R1 + I22R2.
Схемы соединения приёмников электрической цепи.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
studfiles.net
§ 1.6. Применение законов Кирхгофа для описания электрического состояния цепей постоянного тока
Основными законами, используемыми для анализа и расчета электрических цепей, являются первый и второй законы Кирхгофа.
Первый закон Кирхгофаявляется следствием закона сохранения заряда, согласно которому в любом узле заряд одного знака не может ни накапливаться, ни убывать. Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:
2/ = 0. (1.5)
При этом токи, направленные от узла, следует брать со знаком плюс, а токи, направленные к узлу,— со знаком минус.
Второй закон Кирхгофаявляется следствием закона сохранения энергии, в силу которого изменение потенциала в замкнутом контуре равно нулю. Изменение потенциала между двумя точками участка цепи характеризуется разностью потенциалов, которую можно измерить вольтметром. В электротехнике разность потенциалов между двумя любыми точками цепи принято называть напряжением. Поэтому согласно второму закону Кирхгофа алгебраическая сумма напряжений всех участков замкнутого контура равна нулю:
(1.6)
Применительно к схемам замещения с источниками э.д.с. второй закон Кирхгофа можно формулировать таким образом: алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме э.д.с., входящих в этот контурз
(1.6а)
При составлении уравнений (1.6) и (1.6а) слагаемые берут со знаком плюс в случае, когда направление обхода контура совпадает с направлением соответственно напряжения, тока или э.д.с., в противном случае слагаемые берут со знаком минус.
Анализ и расчет любой электрической цепи можно провести на основании применения первого и второго законов Кирхгофа. Рас-
Рис. 1.17. Схема замещения электрической цепи с несколькими источниками э. д. с, (а), граф схемы цепи (б) и дерево графа (в)
смотрим применение законов Кирхгофа для определения токов ветвей цепи (рис. 1.17, а), если сопротивления и э.д.с. всех элементов известны.
Рекомендуется следующий порядок составления уравнений по законам Кирхгофа: определяют число ветвей, узлов и независимых контуров, устанавливают число независимых уравнений по первому закону Кирхгофа, остальные уравнения составляют по второму закону Кирхгофа.
Для определения неизвестных токов в ветвях необходимо составить уравнения по первому й второму законам Кирхгофа, количество которых должно быть равно количеству неизвестных токов. По первому закону Кирхгофа можно составить у—1 независимых уравнений, гдеу— количество узлов цепи. Использовать всеууравнений невозможно, так как одно из них обязательно будет зависимым. Это
связано с тем, что токи ветвей войдут в уравнения, составленные для всех уузлов, дважды, причем с разными знаками, поскольку один и тот же ток направлен от одного узла (имеет знак плюс в уравнении) к другому узлу (имеет знак минус). При сложении всех уравнений левая и правая части будут равны нулю, а это означает, что одно из уравнений можно получить суммированиему—1уравнений и заменой знаков всех токов на противоположные. Таким образом,у-е уравнение всегда будет зависимым и поэтому использовать его для определения токов нельзя.
Количество уравнений, составляемых по первому закону Кирхгофа, равно коли- / честву ветвей любого дерева графа рассматриваемой цепи, так как количество ветвей дерева, как было указано в § 1.5, равно у—1.
Схема электрической цепи рис. 1.17, аимеете пять, ветвей и трй узла, поэтому по первому закону Кирхгофа для нее можно составить "Два^йезависимых ур авнени я, н апр имер:
для узла 1
(1.7)
для узла 2
(1.7а)
/з-/4+ /5^0.Граф рассматриваемой схемы цепи приведен на рис. 1.17, б. Любое дерево этого графа имеету—1=2 ветви, например дерево на рис. 1.17, б.
Количество уравнений, составляемых по второму закону Кирхгофа, должно быть равно количеству независимых контуров. Независимым называют контур, в который входит хотя бы одна новая ветвь.
Очевидно, что каждая связь графа образует новый (независимый) контур, поэтому количество независимых контуров равно количеству связей графа, т. е.
=п—(у—1), гдеп— общее количество ветвей цепи. Граф схемы цепи рис. 1.17,б имеетп=5 ветвей ис—3 связи.
Для схемы цепи рис. 1.17, анадо составить три уравнения по второму закону Кирхгофа для трех независимых контуров. Примем направление обхода контуров по часовой стрелке. Тогда
для контура I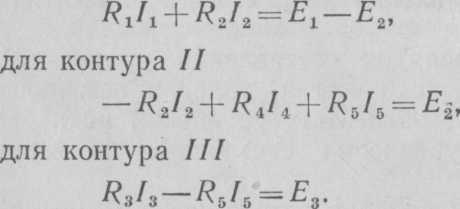
(1.8)
(1.8а)
(1.86)
При составлении уравнений (1.8) — (1.86) со знаком плюс записаны те слагаемые, в которых ток и э.д.с. имеют направления, совпадающие с направлением обхода контура.
Решая систему уравнений (1.7), (1.8), можно определить все пять неизвестных токов. Если в результате решения этих уравнений полу-
чатся отрицательные значения токов, то это означает, что истинные направления токов в ветвях цепи противоположны тем направлениям, для которых составлялись уравнения (1.7), (1.8).
Правильность расчета токов в ветвях электрической цепи может быть проверена с помощью уравнения баланса мощностей источников и приемников электрической энергии:
2 £/=2/?/*, (1.9)
в котором правая часть характеризует мощность пассивных приемников электрической энергии, а левая — мощность активных элементов цепи. При составлении уравнения баланса мощностей следует иметь в виду, что в левой его части со знаком плюс записываются те слагаемые, для которых направления э.д.с. и тока совпадают. Если же направления э.д.с. и тока противоположны, то соответствующие слагаемые записываются со знаком минус в левой части уравнения или со знаком плюс в правой его части, что соответствует мощности активного приемника электрической энергии.
studfiles.net
1. Линейные электрические цепи постоянного тока. 1, 2 законы Кирхгофа.
Последовательность расчета линейных электрических цепей с помощью законов Кирхгофа:
произвольно задаются положительные направления токов в ветвях;
обозначают направления обхода контуров;
записывают уравнения по первому и второму законам Кирхгофа;
решают уравнения;
проверяют правильность расчета, составляя энергетический баланс.
Первый закон Кирхгофа:
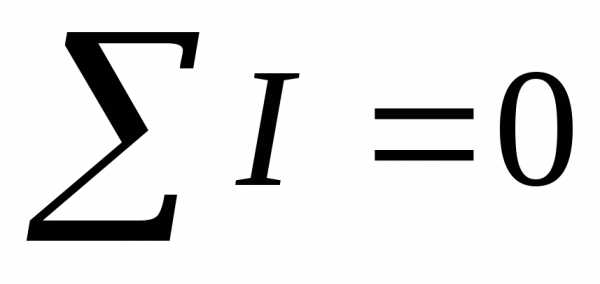
Формулировка:Алгебраическая сумма токов ветвей, сходящихся в узле равна нулю, при этом токи, направленные от узла, следует брать со знаком плюс, а токи, направленные к узлу, - со знаком минус.
Второй закон Кирхгофа:
Формулировка:Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме э.д.с., входящих в контур. Слагаемые берут со знаком плюс в случае, когда направление обхода контура совпадает с направлением соответсвенно напряжения, тока или э.д.с., в противном случае слагаемые берут с отрицательным знаком.
Если в цепи имеется x ветвей и у узлов, в том числе xi –ветвей с источниками токов, то необходимо составить x–xi уравнений для определения токов во всех ветвях. При этом по первому закону Кирхгофа составляют у–1 уравнений, а все остальные x–xi–(у–1) уравнения – по второму закону Кирхгофа.
Для проверки правильности расчетов определяют сумму мощностей, генерируемых источниками, и сравнивают ее с суммой мощностей всех потребителей
.
Слагаемые I2R всегда положительны, а слагаемые EI берут со знаком минус, когда направления E и I встречные. Если баланс не получается, то токи определены неправильно.
2. Методы расчёта электрических цепей постоянного тока.
Метод контурных токов:
Ток в любой ветви электрической схемы можно представить в виде суммы нескольких токов, каждый их которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие действительных токов называют контурными токами. На рис. действительный ток I2 можно представить как разность контурных токов I11 и I22, т.е.
I2=I11–I22 .
При этом уравнение по второму закону Кирхгофа, составленное для 1-го контура, имеет вид I1R1+I2R2=E1–E2, или с учетом предыдущего уравненияI11R1+(I11–I22)R2=E1–E2.
Аналогично для другого контура
I2R2+I3R3=E3–E2 или (I11–I22)R2–I22R3=E3–E2.
Преобразуем уравнения
или иначе I11R11–I22R12=E11
–I11R21+I22R22=E22,
где R11 – сумма сопротивлений всех ветвей, входящих в первый контур; R12 – сопротивление ветви, общей для первого и второго контура; E11 – сумма всех ЭДС, входящих в первый контур.
Соответствующие ЭДС берутся со знаком «минус», если они направлены против направления обхода контура. Аналогичные величины получаются для второго контура.
Метод наложения (суперпозиции):
Для линейных цепей ток в k-ветви равен сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Это позволяет проводить расчеты электрических цепей методом наложения – сначала определить все токи от одной ЭДС, затем от другой и т.д., а потом все составляющие токов от разных ЭДС сложить. Отметим, что мощности от частичных токов суммировать нельзя – в баланс мощностей должны входить полные токи.
Принцип взаимности:
Для линейной цепи ток в k-ветви Ik, вызванный источником Em, находящимся в m-ветви, равен току Im в m-ветви, вызванным источником Em, если источник Em перенести в k-ветвь , т.е. Ik=Emgkm=Emgmk.
Принцип компенсации:
В любой электрической цепи без изменений токораспределения можно заменить сопротивление источником ЭДС, величина которого равна падению напряжения на сопротивлении и направлена встречно току на этом сопротивлении. Аналогичную замену можно сделать и источником тока J, величина которого равна току в этом сопротивлении и направлена на ту же сторону. Это следует из второго и соответственно первого законов Кирхгофа при переносе слагаемого из левой части уравнения в правую.
3. Нелинейные электрические цепи постоянного тока и методы их расчета.
В электрические цепи могут входить элементы, сопротивление которых не является величиной постоянной, а зависит от напряжения и силы тока. Вольт-амперная характеристика (ВАХ) такого элемента имеет нелинейный вид, поэтому элемент называется нелинейным (НЭ). Электрическая цепь, в которую входит хотя бы один нелинейный элемент, называется нелинейной. К нелинейным элементам относятся полупроводниковые приборы, лампы накаливания и др. На рис.1 приведена ВАХ одного из НЭ.
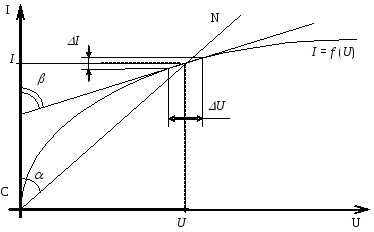
Каждой точке ВАХ НЭ соответствует определенное сопротивление 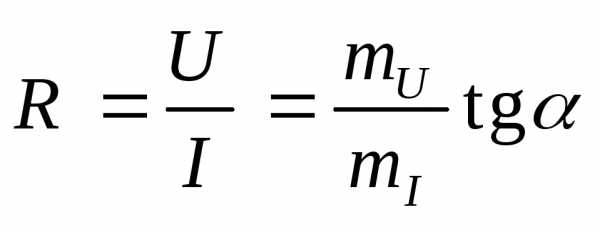 , которое пропорционально тангенсу угла наклона прямой CN к оси токов. Это сопротивление называетсястатическим и представляет собой сопротивление элемента постоянному току. Кроме статического сопротивления НЭ для каждой точки характеристики можно определить так называемое дифференциальное сопротивление Rдиф, которое равно отношению приращения напряжения U к приращению тока I, стремящегося к нулю:
, которое пропорционально тангенсу угла наклона прямой CN к оси токов. Это сопротивление называетсястатическим и представляет собой сопротивление элемента постоянному току. Кроме статического сопротивления НЭ для каждой точки характеристики можно определить так называемое дифференциальное сопротивление Rдиф, которое равно отношению приращения напряжения U к приращению тока I, стремящегося к нулю:
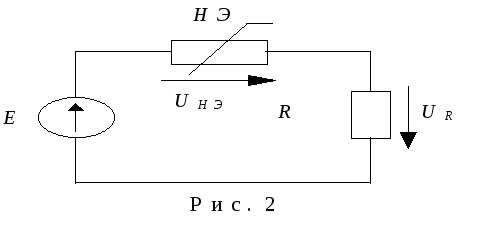
т.е. пропорционально тангенсу угла наклона касательной в данной точке характеристики к оси токов. Дифференциальное сопротивление характеризует НЭ при малых изменениях напряжения и тока. При расчете нелинейной цепи с последовательным соединением линейного и нелинейного элемента часто используют метод нагрузочной характеристики.
Для цепи, показанной на рис. 2, согласно второму закону Кирхгофа можно записать:
,
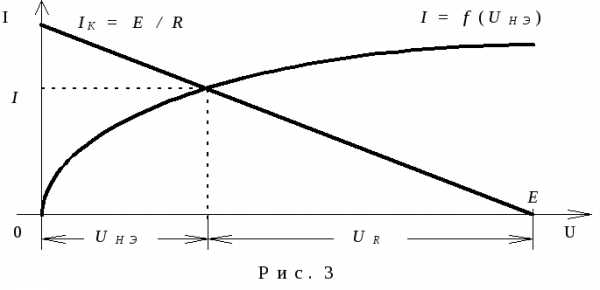
откуда 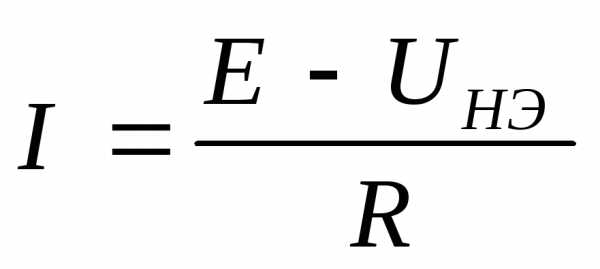 . (1)
. (1)
studfiles.net