ул.Симферопольская
дом 5, офис 9
![]() Корзина
Корзина
Корзина пуста
Как рассчитать индуктивность катушек с замкнутыми сердечниками? Формула расчета катушки индуктивности
формула. Измерение индуктивности. Индуктивность контура
Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.
Электрическая цепь и индуктивность
 Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

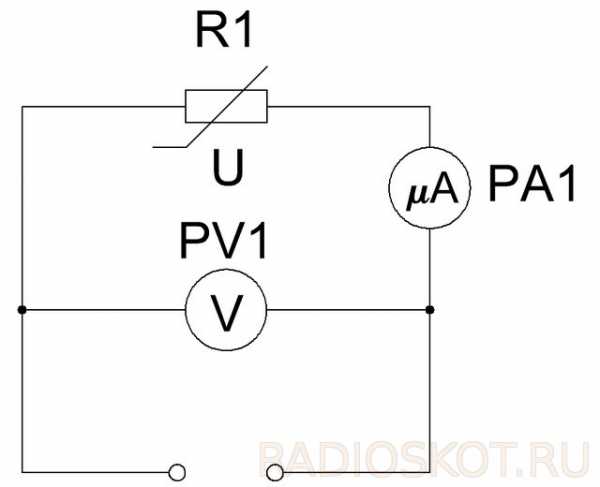
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название "самоиндукция". По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
"Катушка ниток"
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь "катушка – источник тока", то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от "витков в квадрате".
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.
 В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:
В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) - это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Колебательные контуры
Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:
где XL показывает реактивное сопротивление катушки, а W - круговая частота.
Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:
Xc = 1 : W х C.
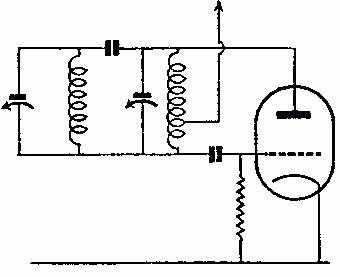 Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
Работа конденсатора
Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:
- Конденсаторы с газообразным диэлектриком.
- Вакуумные.
- С жидким диэлектриком.
- С твердым неорганическим диэлектриком.
- С твердым органическим диэлектриком.
- Твердотельные.
- Электролитические.
Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:
- Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
- Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
- Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
 Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
fb.ru
Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
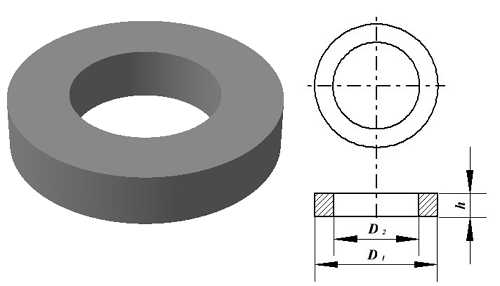 Тороидальный сердечник.
Тороидальный сердечник. Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
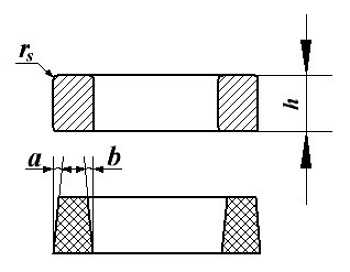 Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу). Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
в) трапецеидальное поперечное сечение с острыми кромками
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
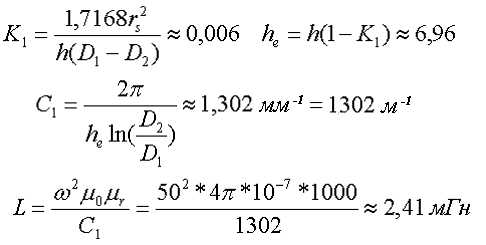
Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
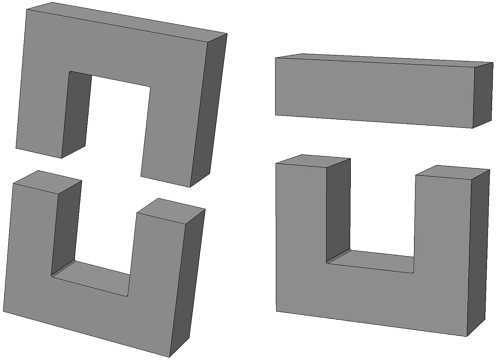 П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа). Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
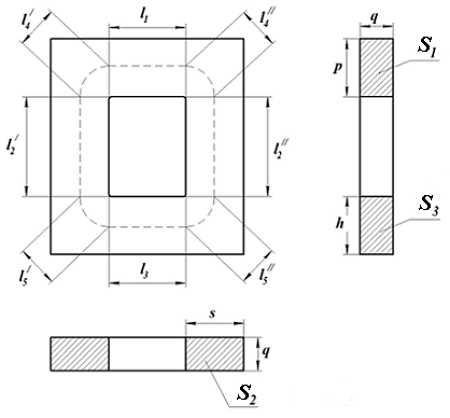 Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят Неизвестные величины можно найти следующим образом
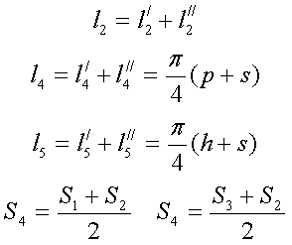
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
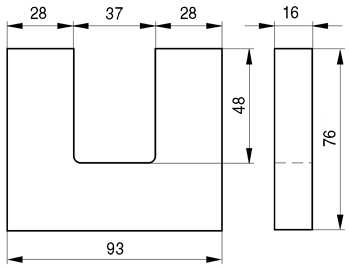 Сердечник Epcos U93/76/16.
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
Таким образом коэффициент С1 и индуктивность L составят
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей
 П-образный сердечник с круговым сечением.
П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
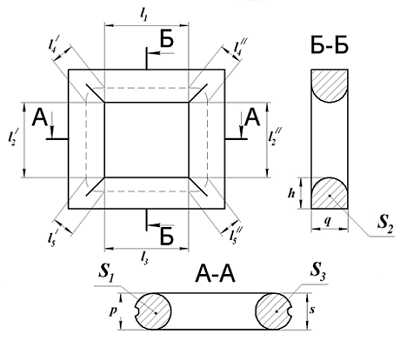 Сечение П-образного сердечника с круговым сечением.
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
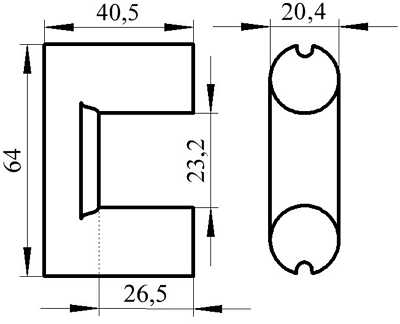 Сердечник типа SDMR 40 UY20.
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
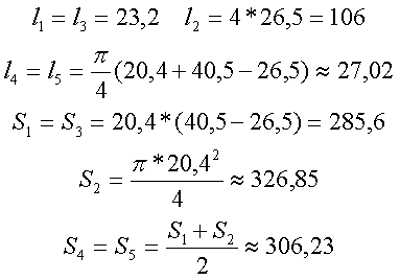
Таким образом коэффициент С1 и индуктивность L составят
На сегодня всё. Продолжение смотри в следующей статье.
Теория это хорошо, но теория без практики - это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками
Скажи спасибо автору нажми на кнопку социальной сети
www.electronicsblog.ru
Расчёт индуктивности. Часть 1 | HomeElectronics
Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.
Методы расчёта индуктивностей
Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается ΨL) и электрическим током, который возбуждает данное потокосцепление.
В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B0 (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления ΨL
где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;
n – количество контуров с током, которые пронизывает магнитный поток.
Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению
где δ – глубина проникновения переменного тока или толщина скин-слоя;
μ – магнитная проницаемость вещества;
γ – удельная электрическая проводимость материала проводника;
ω – круговая частота переменного тока, ω = 2πf.
Поэтому непосредственный способ вычисления индуктивности практически не применяется.
На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.
Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:
индуктивные элементы без сердечников;
индуктивные элементы с замкнутыми сердечниками;
индуктивные элементы с сердечниками, имеющие воздушный зазор.
Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.
Индуктивность прямолинейного провода круглого сечения
При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.
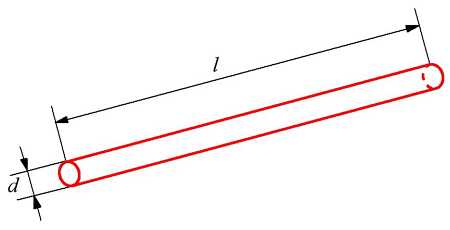 Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.
Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.
В случае постоянного тока или тока низкой частоты индуктивность составит
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
l – длина провода, м;
d – диаметр провода, м.
Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где
d = 2r – диаметр поперечного сечения провода, м.
где ω – угловая частота переменного тока, ω = 2πf;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
γ – удельная проводимость вещества проводника.
Тогда если k*r < 3, то
если k*r > 3, то
где
Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.
На постоянном токе
На частоте 50 кГц
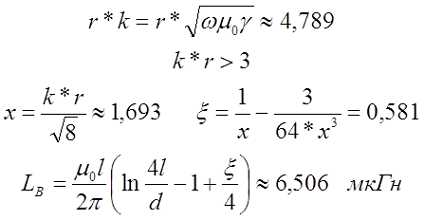
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
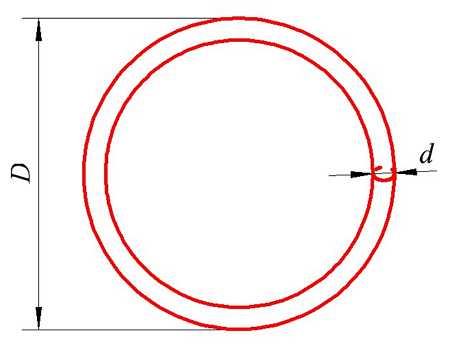 Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).
Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
На частоте 50 кГц
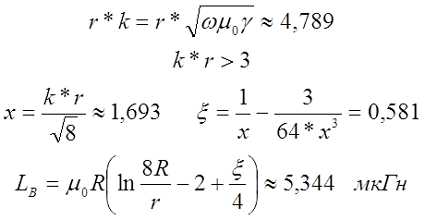
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Теория это хорошо, но теория без практики - это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками
Скажи спасибо автору нажми на кнопку социальной сети
www.electronicsblog.ru
Coil32 - Методы расчета индуктивности катушки.
Методы расчета индуктивностей
 Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: "Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин". Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.
Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: "Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин". Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.
Прежде всего отметим, что расчет индуктивности можно вести двумя способами:
∙ Численный метод с различной степенью упрощения задачи
∙ Расчет по упрощенным эмпирическим формулам
Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.
Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:
- Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести COMSOL Multiphysics, FEMM, ANSYS, GAL-ANA и т.п. Эти программы используют специальные численные методы, такие как метод моментов и метод конечных элементов. Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент [пример]
- Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке Д.К.Максвеллом. Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32...
Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.Из Теоремы Гаусса следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:
Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции [вывод здесь]:
Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:
| [1] |
, где: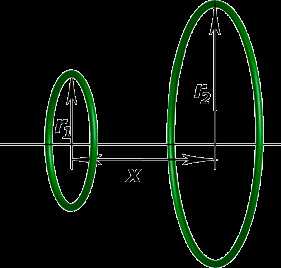
- M - взаимоиндукция;
- r1, r2 - радиусы двух бесконечно тонких круговых проводников;
- x - расстояние между центрами кругов, ограниченных этими проводниками;
- K,E - эллиптические интегралы, соответственно первого и второго рода;
Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.
По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле - это спираль), можно уменьшить с помощью соответствующих поправок.
Рассчитывая взаимоиндукцию проводника "самого на себя", т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие - "среднее геометрическое расстояние" - GDM (g), для круглого провода:
g = e0.25*rw, где rw - радиус провода.
Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса - ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.
Ссылки:
- An introduction to the art of Solenoid Inductance Calculation D W Knight 2013
- Numerical Methods for Inductance Calculation Robert Weaver 2012
- Inductance Calculation Techniques --- Part II: Approximations and Handbook Methods Marc T. Thompson 1999
- A new method for inductance calculation M.A.Bueno A K T Assis 1995
coil32.ru
Расчёт катушки индуктивности под динамик – ldsound.ru
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
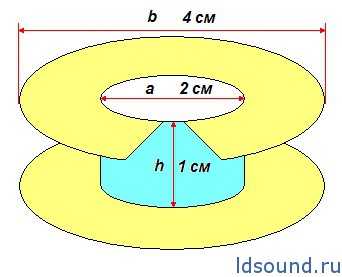
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
- откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
- далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
- длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
- количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
- диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
- масса намотки: m = (h4 х 10-3) / 21,4 = (26,963 х 10-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
- высота намотки h = 26,96 мм;
- значит внутренний диаметр a = 53,92 мм;
- соответственно внешний: b = 107,84 мм;
- длинна жилы: 34,3 м;
- количество витков: 135;
- диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.ru
ldsound.ru
Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)
Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)
Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.
Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.
Расчет однослойных цилиндрических катушек производится по формуле
где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; n—число витков катушки.
При расчете катушки могут встретиться два случая:
а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
б) при известной индуктивности определить число витков и диаметр провода катушки.
В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим в формулу все необходимые величины:
Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и
длину намотки, а затем рассчитывают число витков по формуле
После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле
где d— диаметр провода, мм, l — длина обмотки, мм, п — число витков.
Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.
Подставив в последнюю формулу заданные величины,
получим:
Диаметр провода
Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, также придется увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.
Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам
В.Г.Бастанов, "300 практических советов"
www.radio-schemy.ru
Расчет индуктивности катушек: формула :: ashanet.ru
У каждого из нас бывали проблемы с предметами в школе. У кого-то были проблемы с химией, у кого-то - с физикой. Но даже если с этими предметами у вас всё всегда было хорошо, вы наверняка не помните всех тем, что вам давали в школе. Одной из таких тем является электромагнетизм в целом и расчёт индуктивности катушек в частности.
Для начала окунёмся немного в историю такого явления, как магнетизм.
История
Магнетизм начинает свою историю ещё с Древнего Китая и Древней Греции. Открытый в Китае магнитный железняк использовался тогда в качестве стрелки компаса, указывающей на север. Есть упоминания, что китайский император использовал его во время битвы.
Однако вплоть до 1820 года магнетизм рассматривался лишь как явление. Всё его практическое применение было заключено в указании стрелки компаса на север. Однако в 1820 году Эрстед провёл свой опыт с магнитной стрелкой, показывающий влияние электрического поля на магнит. Этот опыт послужил толчком для некоторых учёных, взявшихся за это всерьёз, чтобы разработать теорию магнитного поля.
Спустя всего 11 лет, в 1831 году, Фарадей открыл закон электромагнитной индукции и ввёл в обиход физиков понятие "магнитное поле". Именно этот закон послужил основой для создания катушек индуктивности, о которых сегодня и пойдёт речь.
А прежде чем приступить к рассмотрению самого устройства этих катушек, освежим в голове понятие магнитного поля.

Магнитное поле
Это словосочетание знакомо нам со школьной скамьи. Но многие уже забыли о том, что оно означает. Хотя каждый из нас помнит, что магнитное поле способно воздействовать на предметы, притягивая или отталкивая их. Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом - "электромагнитные явления". На самом деле электромагнетизм - довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, - это очень малая часть того, что известно человечеству о магнетизме сегодня.
А сейчас перейдём непосредственно к предмету нашей статьи. Следующий раздел будет посвящён рассмотрению непосредственно устройства катушки индуктивности.

Что такое катушка индуктивности?
Мы сталкиваемся с этими предметами постоянно, но вряд ли придаём им какое-то особое значение. Это для нас обыденность. На самом деле катушки индуктивности встречаются сегодня практически в каждом приборе, но наиболее яркий пример их использования - трансформаторы. Если вы думаете, что трансформаторы бывают только на энергетических подстанциях, то вы сильно ошибаетесь: ваше зарядное устройство от ноутбука или смартфона - тоже своего рода трансформатор, только меньшего размера, чем те, что используются на электростанциях и распределительных подстанциях.
Любая катушка индуктивности состоит из сердечника и обмотки. Сердечник представляет собой стержень из диэлектрического или ферромагнитного материала, на который наматывается обмотка. Последняя делается чаще всего из медной проволоки. Количество витков обмотки напрямую связано с величиной магнитной индукции полученной катушки.
Теперь, прежде чем рассмотреть расчет индуктивности катушек и формулы, необходимые для него, поговорим о том, какие параметры и свойства мы будем вычислять.

Какие параметры есть у катушки?
Катушка обладает несколькими физическими характеристиками, отражающими её качество и пригодность для той или иной работы. Одной из них является индуктивность. Она численно равна отношению потока магнитного поля, создаваемого катушкой, к величине этого тока. Индуктивность измеряется в Генри (Гн) и в большинстве случаев принимает значения от единиц микрогенри до десятков Генри.
Индуктивность является, пожалуй, самым важным параметром катушки. Поэтому неудивительно, что большинство людей даже не думают о том, что существуют другие величины, способные описывать поведение катушки и отражать её пригодность для того или иного применения.
При выборе катушки индуктивности профессионалы также обращают внимание на сопротивление потерь. Как можно понять из этого словосочетания, оно отражает величину потерь электроэнергии, происходящих вследствие паразитных эффектов, таких как, например, нагревание проводов, происходящее по закону Джоуля-Ленца. Нетрудно понять, что чем ниже это значение для катушки, тем она лучше.
Ещё один параметр, который необходимо учитывать, - добротность контура. Она тесно связана с предыдущим параметром и представляет собой отношение реактивного сопротивления к активному (сопротивлению потерь). Соответственно, чем выше добротность - тем лучше. Её повышение достигается за счёт выбора оптимального диаметра провода, материала и диаметра сердечника, числа обмоток.
Сейчас рассмотрим подробнее самый важный и наиболее волнующий нас параметр - индуктивность катушки.

Немного больше про индуктивность
Мы уже разобрали это понятие, и теперь осталось поговорить о нём немного подробнее. Зачем? Нам ведь предстоит расчет индуктивности катушек, а значит, необходимо понимать, что это такое и зачем нам её рассчитывать.
Катушка индуктивности предназначена для создания магнитного поля, а значит, имеет параметры, которые описывают его силу. Таким параметром является магнитный поток. Но разные катушки имеют разные потери при прохождении через них тока и, соответственно, разный КПД. В зависимости от диаметра проводов и количества витков катушка может давать разное по величине магнитное поле. Значит, необходимо ввести такую величину, которая бы отражала зависимость между величиной магнитного потока и силой тока, пропускаемой через катушку. Таким параметром и является индуктивность.

Зачем нужен расчёт индуктивности?
Катушек разных видов в мире достаточно много. Они отличаются между собой свойствами, а значит, и применениями. Одни используются в трансформаторах, другие, соленоиды, выполняют роль электромагнитов большой силы. Кроме этих, применений у катушек индуктивности найдётся предостаточно. И для всех них необходимы разные типы катушек. Они отличаются по своим свойствам. Но большую часть этих свойств можно объединить с помощью понятия индуктивности.
Мы уже близко подошли к объяснению того, что включает в себя формула расчета индуктивности катушки. Но стоит оговориться, что речь пойдёт не о "формуле", а о "формулах", так как все катушки можно разделить на несколько больших групп, для каждой из которых своя отдельная формула.

Виды катушек
По функциональности различают контурные катушки, находящие применение в радиофизике, катушки связи, используемые в трансформаторах, и вариометры, то есть катушки, показатели которых можно варьировать изменением взаимного расположения катушек.
Также существует такой вид катушек, как дроссели. Внутри этого класса также есть деление на обычные и сдвоенные. Они имеют высокое сопротивление переменному току и очень низкое - постоянному, благодаря чему могут служить хорошим фильтром, пропускающим постоянный ток и задерживающим переменный. Сдвоенные дроссели отличаются большей эффективностью при больших токах и частотах по сравнению с обычными.
Формулы расчёта
Пришла пора нам перейти к основной теме статьи. Начнём мы с того, что расскажем о том, как произвести расчет индуктивности катушки без сердечника. Это самый простой вид расчёта. Но тут тоже есть свои тонкости. Возьмём, для простоты, катушку, обмотка которой лежит одним слоем. Для неё справедлив расчет однослойной катушки индуктивности:
L=D2*n2/(45D+100l).
Здесь L - индуктивность, D - диаметр катушки в сантиметрах, n - число витков, l - длина намотки в сантиметрах. Однослойная катушка предполагает то, что толщина намотки будет не больше одного слоя, а значит, для неё справедлив расчет плоской катушки индуктивности. В целом большинство формул для расчётов индуктивностей очень похожи: существенные различия только в коэффициентах при переменных в числителе и знаменателе. Самым простым тут является расчет индуктивности катушки без сердечника.
Представляет интерес также формула расчета индуктивности катушки с большим числом витков:
L=0,08*D2*n2/(3*D+9*b+10*c).
Здесь b - ширина провода, c - его высота. Такая формула эффективна для того, чтобы произвести расчет многослойной катушки индуктивности. Применяется она на практике чуть менее часто, чем та, о которой пойдёт речь ниже.
Самым актуальным, пожалуй, будет расчет индуктивности катушки с сердечником. Есть специальная формула, которая показывает, что эта индуктивность определяется материалом, из которого сделан сердечник, а точнее - его магнитной проницаемостью. Выглядит эта формула так:
L=m*m0*n2*S/l,где m - магнитная проницаемость материала сердечника, m0 - магнитная постоянная (она равна 12,56·10-7 Гн/м), S - площадь поперечного сечения катушки, l - длина намотки.
Расчет витков катушки индуктивности производится очень просто: это число намотанных на сердечник слоёв проводника.
Мы разобрались с формулами, а теперь немного о том, где же конкретно эти формулы и расчёты могут нам пригодиться.

Практическое применение
Эти формулы имеют очень широкое применение ввиду повсеместного распространения катушек индуктивности. Как мы уже выяснили, бывают разные виды катушек, каждый из которых соответствует своему применению. В связи с этим становится необходимым как-то разделять их по характеристикам, ведь для каждой отрасли необходима своя определённая индуктивность и добротность.
В основном расчет индуктивности катушек применяется на производстве и в электротехнике. Каждый радиолюбитель должен знать, как производить расчет индуктивности, иначе как ему определить, какая катушка из огромного множества подойдёт для его цели, а какая - нет.
Вам интересно?
Сегодня очень много учёных, интересующихся магнетизмом и магнитными явлениями. Они изучают как магнитную, так и электрическую стороны веществ, пытаясь выявить закономерности и синтезировать мощные магниты с определёнными нужными свойствами: например, с высокой температурой плавления или сверхпроводимостью. Все эти материалы могут быть использованы в огромном количестве отраслей.
Приведём пример с аэрокосмической отраслью: перспективными для дальних межзвёздных перелётов являются ракеты с ионными двигателями, которые создают тягу посредством выброса ионизированного газа из сопла. Сила толчка в таком двигателе зависит от температуры газа и скорости его движения. Соответственно, чтобы придать газу максимальную силу для разгона, нам требуется очень сильный магнит, разгоняющий заряженные частицы и к тому же имеющий очень высокую температуру плавления для того, чтобы не расплавиться при выходе газов из сопла.
Заключение
Знание никогда не бывает лишним и всегда где-нибудь, да пригодится. Теперь, если вам попадётся программа расчета индуктивности катушки, вы без труда сможете сказать, почему там именно такие формулы и какие переменные в них что означают. Эта статья предназначена лишь для вашего ознакомления, и если вы хотите знать больше, стоит почитать специализированную литературу (благо за много лет изучения магнитных явлений её накопилось очень много).
ashanet.ru